AMC 8/10/12 EXAM PREP
The first step to admission at
|
|
Show off your skills by applying to your dream school with a great AMC score. Achievable is the only AMC exam prep course that uses memory science technology to ensure you reach your goal.
Achievable's AMC courses are authored by Wes Carroll, who has been helping AIME hopefuls realize their ambitions for over two decades.
You'll love studying with Achievable
Thousands of students trust Achievable exam prep to help them pass their most important exams
95%+
Success rate
50M+
Questions answered
2M+
Hours studied
Achievable has been absolutely amazing thus far! The material is very easy to comprehend and I Now feel very prepared for the exam!
Been studying for this for a week and this helped me more than the 300-page textbook I read. Thank you. I've been studying for these exams for almost 6 months and have been SO confused. Now I understand! Wow! you made it so clear! Thank you so much!
Site is easy to navigate and offers a good deal of study material.
Achievable is the best resource I've found. More so than with [competitor], or [competitor] I find the material "sticks" with Achievable's system of introducing new material, followed by review quizzes to master previous readings. It's incredibly easy to use, anywhere you are (at home on a desktop, laptop, or away with your mobile device) and actually interesting to read. Every other guide I've tried reads like stereo instructions.
Great job explaining concepts in enough detail to understand them and feel prepared and confident to take the exam.
I am pleasantly surprised at the quantity and quality of information supplied by achievable. I was skeptical at first, but after spending time with them I i highly recommend using them. If you are looking for more detailed information I would suggest looking somewhere else, but honestly all you need are the basics.
This has helped me tremendously. The on hands learning with videos as well is a different type of mental learning.
User friendly with lots of applicable information. Questions are similar to the actual exam.
Crucial fundamentals
Too many AMC hopefuls study the wrong fundamentals, in the wrong order. Our Achievable AMC study materials have been carefully curated by our expert partner Wes Carroll to include everything you need to keep you from stumbling or plateauing later.
Unparalleled retention
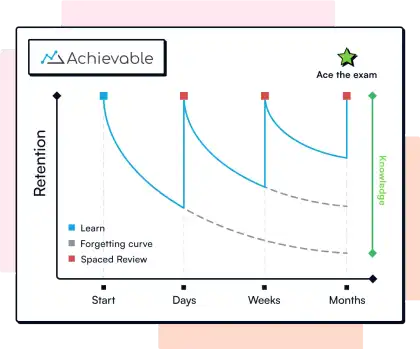
Achievable AMC exam prep uses adaptive learning techniques to create and update a personalized model of your memory, individually tracking your retention and mastery of each AMC learning objective. Our learning engine monitors your study progress and continually adjusts your quiz questions to ensure you're focusing on the topics that matter most for you, improving study effectiveness and retention, while drastically reducing overall study time.
No fluff
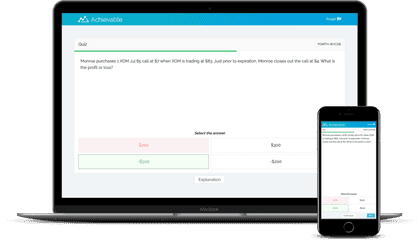
Continually reviewing the material you've learned while studying is essential, but you need more than simple AMC flashcards. Other courses pad their materials with important-sounding but ultimately unnecessary material and verbiage. We know that you are an ambitious and busy student. That's why our AMC online course contains everything you need to understand the AMC sections, but nothing you don't.
Easy to work with on all platforms
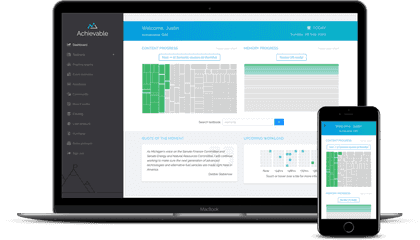
You'll see within minutes why our online textbook and platform are a cut above other AMC exam prep. Everything is easy to understand and written in plain English, filled with straightforward explanations and test-appropriate examples. Whether you're studying on the web or a smartphone, the Achievable AMC exam prep platform UX is clean and responsive. Progress charts highlight your journey through the AMC course content and your current strength in each section.
How is this different from AoPS?
The team and community at AoPS have done a great job of providing a huge volume of high-quality resources for preparing for the AMC tests, and we are grateful for their work both in helping to build champions, and also in raising awareness about the AMC. That's no exaggeration.
But in contrast to their broader mission, our Achievable AMC course has only one purpose: to give students the shortest possible path to knowing all the needed facts, formulas, and concepts, and having them down absolutely cold.
Our course graduates will correctly tell you that everything in this course is available elsewhere in principle. But now it's available all in one place, built into a customizable learning engine that automatically adjusts to your demonstrated knowledge level. That makes this one component of AMC mastery accessible in months instead of years, while taking far less total time away from other activities.
AMC 8 Key stats
Questions
25
Length
40 minutes
Format
Multiple choice
Eligibility
Children in grade 8 or below and under 14.5 years of age on the day of the competition
Why take the AMC 8?
The AMC 8 is for middle school students that are interested in developing a proficiency for mathematics and analytical thinking. The journey that begins with the AMC 8 can lead to further mathematics competitions (such as the AMC 10 and 12), an improved college application, or assistance in future careers. Students apply the skills they already learn in middle school math class to unique challenges that test their problem solving and critical reasoning.
What's on the AMC 8?
The material covered on the AMC 8 should be included in a typical middle school mathematics curriculum, but is not usually covered at this level of depth. Possible topics include (but are not limited to): counting and probability, estimation, proportional reasoning, elementary geometry including the Pythagorean Theorem, spatial visualization, everyday applications, and reading and interpreting graphs and tables. Some of the more challenging questions may involve linear or quadratic functions and equations, coordinate geometry, and other topics traditionally covered in a beginning algebra course.
AMC 10 Key stats
Questions
25
Length
75 minutes
Format
Multiple choice
Eligibility
Children in grade 10 or below and under 17.5 years of age on the day of the competition
Why take the AMC 10?
The AMC 10 is for students in the first half of high school that are interested in developing a proficiency for mathematics and potentially competing in the AIME (American Invitational Mathematics Examination) for a spot on the US Math Olympiad Team. Even students who don't make it to the AIME find that the AMC 10 is a great opportunity for them to further their interest in mathematics, tackle advanced problems, and bolster their college application.
What's on the AMC 10?
The material covered on the AMC 10 is often included in a typical grade 9 and grade 10 mathematics curriculum, but almost never at this level of depth. Possible topics include (but are not limited to): elementary algebra, basic geometry knowledge, the Pythagorean Theorem, area and volume formulas, elementary number theory, and elementary probability.
What is NOT included in the AMC 10 is: trigonometry, advanced algebra, advanced geometry, precalculus, or calculus.
AMC 12 Key stats
Questions
25
Length
75 minutes
Format
Multiple choice
Eligibility
Children in grade 12 or below and under 19.5 years of age on the day of the competition
Why take the AMC 12?
The AMC 12 is for high school students that are interested in developing a proficiency for mathematics and potentially competing in the AIME (American Invitational Mathematics Examination) for a spot on the US Math Olympiad Team. Even students who don't make it to the AIME find that the AMC 12 is a great opportunity for them to further their interest in mathematics, tackle advanced problems, and significantly bolster their college application. The AMC 12 is particularly useful for supporting applications to STEM-focused programs at undergraduate universities, especially as the ACT and SAT continue to become less useful to elite universities' admissions departments.
What's on the AMC 12?
Much of the material covered on the AMC 12 is included in most high school mathematics curricula through grade 12. However, almost no schools cover all this material at this level of depth. Possible topics include (but are not limited to): elementary algebra, first- and second-year geometry, elementary number theory, elementary probability, trigonometry, advanced algebra, advanced geometry, and precalculus. Calculus is never included.
AMC exam details
AMC 8
The AMC 8 is a multiple choice examination in middle school mathematics designed to promote the development of problem-solving skills.
The material covered on the AMC 8 includes topics from a typical middle school mathematics curriculum. Possible topics include but are not limited to: counting and probability, estimation, proportional reasoning, elementary geometry including the Pythagorean Theorem, spatial visualization, everyday applications, and reading and interpreting graphs and tables. In addition some of the later questions may involve linear or quadratic functions and equations, coordinate geometry, and other topics traditionally covered in a beginning algebra course.
AMC 12
The AMC 12 covers the entire high school curriculum including trigonometry, advanced algebra, and advanced geometry, but excluding calculus. Students in grade 12 or below and under 19.5 years of age on the day of the contest can take the AMC 12.
The AMC 12 assumes knowledge of elementary algebra; basic geometry knowledge including the Pythagorean Theorem, area and volume formulas; elementary number theory; and elementary probability.
The AMC exam is hosted by MAA. Participants have 40 minutes (AMC 8) and 75 minutes (AMC 12) to answer 25 multiple-choice questions (AMC 8 and AMC 12).
Learn from the best

Our content was written exclusively for Achievable by Wes Carroll, widely considered one of the very best private AMC tutors in the nation. Wes has helped students master the AMC and reach the AIME for over 20 years.
Reach your target score
Achievable is the best online AMC exam prep course: effective, personalized, and convenient. With Achievable, you'll spend less time studying and hit your target score with confidence.